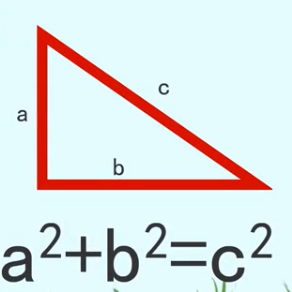勾股定理证明方法七

勾股定理是初中几何中重要的一个三角形定理，在我们的学习和工程实践中应用非常广泛，下面我来看看这个定理是汝河推导出来的。

如上图所示，作一个直角三角形ABC，a、b分别为它的两条直角边，c为斜边。再分别以三条边为边长做正方形，使点H、C、B和A、C、G分别在一条直线上。连接BF、CD，过点C作CL垂直于DE交AB于点M，交DE于点L。

由上图可知：

1、AF=AC，AB=AD，∠CAD=∠FAB=90°+∠CAB，所以三角形FAB全等于三角形CAD，

2、三角形FAB与正方形FACH等底等高，所以三角形FAB的面积等于½a²

3、三角形CAD与四边形ADLM等底等高,所以三角形CAD的面积等于四边形ADLM面积的一半

所以四边形ADLM面积=a²。同理，连接CE和AK可得四边形BELM面积=b²。

由此可得正方形ABDE的面积等于a²+b²，又根据正方形面积公式可得正方形ABDE的面积等于c²

所以a²+b²=c²。