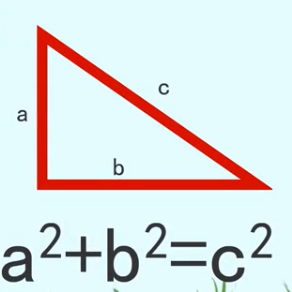勾股定理证明方法六

勾股定理是几何数学中一个重要的三角形定理，为我们求周长和求面积都提供了很多的便利，那么这个定理是如何被求证的呢？下面我们用四个全等的直角三角形来验证一下。

这一次我们换一个思路，我们分别以直角三角形的三边为边长拼出三个正方形。如上图所示，作4个以a、b为直角边，c为斜边的全等直角三角形，将它们拼成如图所示的多边形，使点D、E、F在一条直线上，过点C作AC的延长线与DF相交于点P。

1、设多边形GHCBE的面积为s

2由上图可知，四边形CBDP是边长为a的正方形，四边形GHPF是边长为b的正方形

多边形GHCBDF的面积等于a²+b²=s+½ab×2

正方形ABEG的面积等于c²=s+½ab×2

由此可得a²+b²=c²。