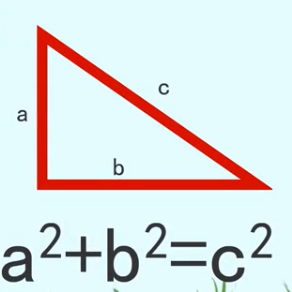勾股定理证明方法四

勾股定理是一个基本的且非常重要的几何定理，本文我们将通过相似三角形的原理来证明这个定理，此法需要在三角形内部做垂直辅助线。

如上图所示，直角三角形的三边分别为a、b、c，我们通过点C向AB作垂线相交于点D

由内角和定理可得∠A+∠B=90°，∠A+∠ACD=90°，所以∠B=∠ACD，三角形ACD与三角形ABC为相似三角形

由此可得AD/AC=AC/AB，AC²=AD×AB

同理三角形BCD与三角形BAC也为相似三角形，BD/BC=BC/AB，BC²=BD×AB

由此可得，AC²+BC²=AD×AB+BD×AB，AC²+BC²=(AD+BD)×AB=AB²，所以a²+b²=c²。