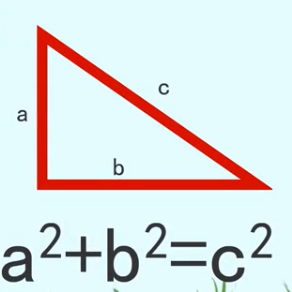勾股定理证明方法三

一直以来都有人不断的给出勾股定理新的证明方法，前面我们已经整理了两种较为简便的方法，下面我们再为大家介绍一种更为简便的方法。这种证明方法只需要用到两个全等的直角三角形，下面我们一起来看看。

如上图所示，用2个以a、b为直角边，c为斜边的全等直角三角行拼成一个梯形，使点AEB在一条直线上。

由于2个直角三角形是全等三角形，所以∠AED=∠ECB，根据内角和定理，∠CEB+∠ECB=90°，所以∠CEB+∠AED=90°，所以，∠DEC=180°-90°=90°，所以三角形DEC是以c为直角边的等腰直角三角形。

下面我们就来求梯形ABCD的面积

根据梯形的面积公式可得梯形ABCD的面积等于½(a+b)×(a+b)=½a²+½b²+ab

同时梯形ABCD的面积又等于3个三角形的面积之和，即等于½c²+½ab×2=½c²+ab

由此可得½a²+½b²+ab=½c²+ab；等式两边简化得a²+b²=c²。