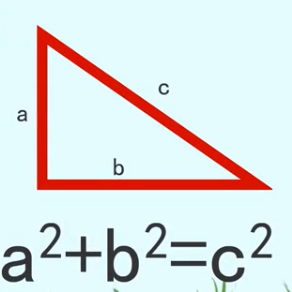勾股定理求最短距离之计算法

求平面中的最短距离有很多方法，本题为大家介绍最直接的一种方法，计算法。

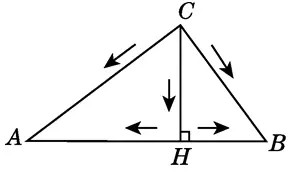
例：如图，A，B两块试验田相距200m，C为水源地，AC＝160m，BC＝120m，为了方便灌溉，现有两种方案修筑水渠．

甲方案：从水源地C直接修筑两条水渠分别到试验田A，B；

乙方案：过点C作AB的垂线，垂足为H，先从水源地C修筑一条水渠到线段AB上的H处，再从H分别向试验田A，B修筑水渠．

(1)试判断△ABC的形状，并说明理由．

(2)两种方案中，哪一种方案所修的水渠较短？请通过计算说明。

解题思路

（1）由勾股定理的逆定理即可得出△ABC是直角三角形；

（2）利用等面积法，由△ABC的面积求出斜边AB上的高CH的长，得出AC＋BC

解析

已知AC＝160m，BC＝120m，AB=200m，通过计算可得AC²+BC²=AB²，根据勾股定理的逆定理可得△ABC为直角三角形，∠ACB=90°。

根据等面积法有S△ABC=½AC×BC=½AB×CH，求出CH=96m。

CH+AH+BH=96m+200m=296m，AC+BC=160m+120m=280m，所以AC+BC＜CH+AH+BH，所以甲方案修建的水渠较短。