勾股定理练习题五

如图，三角形ACB和ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB上一点。(1)求证△ACE≌△BCD，(2)若AD=5，BD=12，求DE的长。

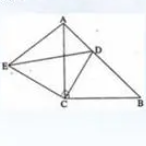
解析

问题1

1、已知三角形ACB和ECD都是等腰直角三角形，所以AC=BC，EC=DC。

2、已知∠ACB=∠ECD=90°，即∠ACD+∠DCB=∠ACD+∠ACE=90°，∠DCB=∠ACE。

3、综合以上两个条件，我们发现三角形ACE和三角形BCD有2条边相等，并且这两条边所夹的角相等，所以这两个三角形是全等三角形，即ACE≌△BCD。

问题2

上面得出ACE≌△BCD，所以AE=BD=12，∠CAE=∠CBD，因为∠ACB=90°，所以∠CBD+∠CAD=90°，即∠CAE+∠CAD=90°，即∠EAD=90°，三角形EAD为直角三角形。根据勾股定理可得AD²+AE²=DE²，5²+12²=DE²，DE=13。