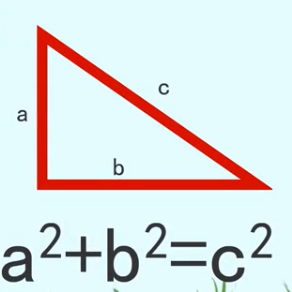勾股定理练习题四

已知三角形ABC的三边分别为a、b、c，且满足a²+b²+c²+50=6a+8b+10c，求三角形ABC的面积。

解析

1、我们将已知条件中的等式变一下形，得到a²+b²+c²+50-6a-8b-10c=0。

2、再将其变一下形得到a²-6a+9+b²-8b+16+c²-10c+25=0

3、再通过完全平方公式将其变一下形得到(a-3)²+(b-4)²+(c-5)²=0

4、我们知道任何一个数的平方都大于或者等于0，上一步中3个数的平方和等于0，也就是三个大于或者等于0的数相加等于0，那么只有一个可能就是三个数都为0，因此a-3=0，b-4=0，c-5=0，由此得到a=3，b=4，c=5，a²+b²=c²。

三角形两边的平方和等于第三边的平方，根据勾股定理的逆定理可得三角形ABC为直角三角形，a、b为直角边，c为斜边。

所以，S△ABC=½3×4=6。