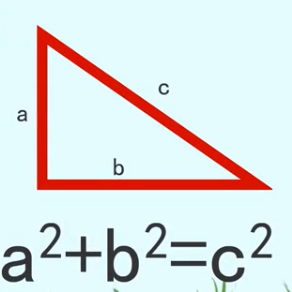首页>题库 > >勾股定理练习题三

勾股定理练习题三

来源：五加一数学原创文章2024-05-10 17:38:35编辑：沐沐

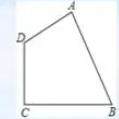
如图有四边形ABCD，已知AB=24，BC=15，CD=20，DA=7，BC⊥CD，求四边形ABCD的面积。

解析

连接BD，已知BC⊥CD，则△BCD为直角三角形，根据勾股定理可得BC²+CD²=BD²，BD=25

又已知AB=24，DA=7，经计算可得AB²+DA²=BD²，根据勾股定理的逆定理可得△ABD也为直角三角形，且DA⊥AB

由图可知四边形ABCD的面积等于S△BCD+S△ABD，即四边形ABCD的面积=½15×20+½7×24=234。

关注五加一数学微信公众号

更多数学公式定理，奥数题库，一题多解，巧解秒解

请关注微信公众号：五加一数学直接扫描右侧二维码关注

分类：初中八年级几何标签：三角形直角三角形直角三角形定理

相关内容