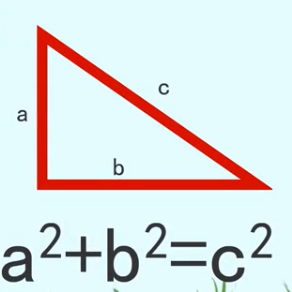勾股树，用勾股定理画出的毕达哥拉斯树

勾股树也称为达哥拉斯树，是由古希腊数学家毕达哥拉斯，利用勾股定理所画出的一个无限重复图形，当重复的次数够多时，就会形成一个树的形状，所以称之为“勾股树”。

勾股树的相关结论

1、两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。

验证：这个结论显而易见，直接勾股定理a²+b²=c²就得出结论。

2、三个正方形之间的三角形，其面积小于等于大正方形面积的四分之一，大于等于一个小正方形面积的二分之一。

验证：

①设两个小正方形的边长分别为a和b，大正方形的边长为c，则有a²+b²=c²。三个正方形之间的三角形面积为½ab，因为任何数的平方大于等于0，所以(a-b)²≥0，a²+b²-2ab≥0，a²+b²≥2ab，¼(a²+b²)≥½ab，反过来就是½ab≤¼(a²+b²)，即½ab≤¼c²，所以三个正方形之间的三角形，其面积小于等于大正方形面积的四分之一。

②当a＜b时，½ab≥½a²，当a＞b时，½ab≥½b²。

毕达哥拉斯树的简单画法

众所周知勾股定理就是直角三角形的两个直角边的平方和，等于斜边的平方，毕达哥拉斯利用这一点，在初始的大正方形上，做出了两个全等的小正方形，在以此类推，无限重复的做出各种大小不一的正方形，就形成了茂密的“毕达哥拉斯树”。

由于三个正方形的内部形成了一个等腰直角三角形，所以通过勾股定理可得，小正方形的边长是大正方形的√2/2，再通过对小正方形重复上述过程，无限重复下去。如果假设其中的大正方形边长为1，在增加到第n 次时，会增加2n个小正方形，而每个小正方形的边长就是√2/2，则每一次增加的面积就是2n×(√2)=1。

从每一个图中两个较小的正方形出发，又可以分别作出一个第三代的勾股定理图，就这样一生二、二生四、四生八，继续繁殖下去，就长成了一棵大树，整棵大树完全是由勾股定理图形组成的，把它叫做勾股树，名副其实，非常恰当。通过改变第一代勾股定理图中直角三角形三边的比例，或者在繁殖过程中适当改变两条直角边的方向，可以得到不同图形的勾股树，就是另外一幅美丽的勾股树形图。

毕达哥拉斯树是无限的吗？

理论上来看，毕达哥拉斯树是可以无限重复的，因为将上述的公式中的n设为无限次后，毕达哥拉斯树的面积就会趋于无限大。勾股树的面积也会更加茂密，但是在现实中并非如此。

因为当n大于5时，所有产生的小正方体互相重叠，所以毕达哥拉斯树的面积其实是有限的。因此毕达哥拉斯树其实只能生长在一个6×4的方格中里，当然具体的值不太容易求出。

感叹数学之美

罗素曾这样评价数学：如果正确地看它，不但拥有真理，而且也具有至高的美，正像雕刻的美，是一种冷而严肃的美。让我们以数学文化为平台，化“冰冷的魅力”为“火热的思考”！