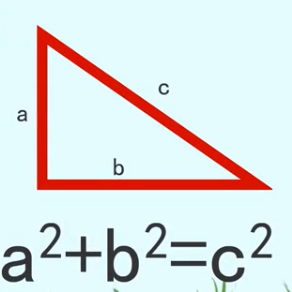勾股定理在数学中可以用来解决哪些问题？

勾股定理是数学中一个非常重要的定理，它描述了直角三角形的三条边之间的关系，具体来说，就是直角三角形的两条直角边的平方和等于斜边的平方。那么勾股定理在数学中具体可以用来解决哪些问题呢？

勾股定理可以用来解决很多关于直角三角形的数学问题，下面五加一学数学的小编为大家罗列几种常见的问题：

1、求斜边长

如果已知直角三角形的两条直角边长，要求斜边长，可以使用勾股定理，具体来说，设直角边长分别为 a 和 b，斜边长为 c，则有：c² = a² + b²。

例：已知直角三角形的两条直角边长分别为 3 和 4，求斜边长，则有：c² = 3² + 4² = 9 + 16 = 25，c = √25 = 5。

2、求直角边长

如果已知直角三角形的斜边长和其中一条直角边长，要求另一条直角边长，也可以使用勾股定理。

例：已知直角三角形的斜边长为 5，其中一条直角边长为 3，求另一条直角边长，则有：b² = c² - a² = 5² - 3² = 25 - 9 = 16，b = √16 = 4。

3、求周长

如果已知直角三角形的其中两条边的长，要求直角三角形的周长，则可以使用勾股定理先求出直角三角形另一条边的长，再将三条边的长度相加得到直角三角形的周长。

例：已知直角三角形的两条直角边长分别为 3 和 4，求周长，则有：c² = 3² + 4² = 9 + 16 = 25，c = √25 = 5，周长=3+4+5=12。

注意：这里已知了两条直角边长分别为 3 和 4，如果没有说明是直角边的话，还有一种情况就是4为斜边，先求出另一条直角边，再求周长，切记最长的边为斜边。

4、求直角三角形的面积

如果已知直角三角形的一条直角边长和斜边长，可以使用勾股定理求出另一条直角边长，再使用三角形面积公式来求出直角三角形的面积。

例：已知直角三角形的斜边长为 5，其中一条直角边长为 3，求直角三角形的面积，则有：b² = c² - a² = 5² - 3² = 25 - 9 = 16，b = √16 = 4，面积=½3×4=6。

5、判断一个三角形是否是直角三角形

如果已知一个三角形的三条边长，要判断它是否是直角三角形，可以使用勾股定理。具体来说，设三角形的三条边长分别为 a、b、c，如果满足勾股定理的条件 a² + b² = c²，则这个三角形是直角三角形，否则不是。我们通常也把这叫做勾股定理的逆定理。

例：已知一个三角形的三条边长分别为 3、4、5，要判断它是否是直角三角形，则有：3² + 4² = 9 + 16 = 25 = 5²，因此这是一个直角三角形。

小编总结

勾股定理可以用来解决很多有关直角三角形的问题，例如求斜边长、求直角边长、求周长，判断一个三角形是否为直角三角形等。我们在使用的过程中一定要注意，最长的边为斜边，要看清题意有没有指明某条边为直角边。