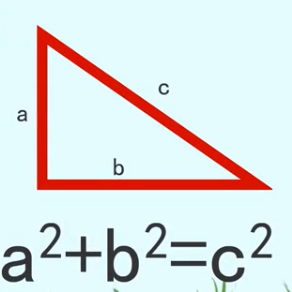勾股定理的逆定理

在数学的学习和研究中我们常常要学会举一三反，正反推理，那么勾股定理的逆定理是什么呢？如果三角形三边长a，b，c满足a²+b²=c²，那么这个三角形是直角三角形，其中c为斜边。

注意事项

1、勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和与较长边的平方作比较，若它们相等时，以a，b，c 为三边的三角形是直角三角形；若a²+b²a²+b²>c²时，以a，b，c 为三边的三角形是锐角三角形；

2、定理中a，b，c 只是一种表现形式，不可认为是唯一的，如若三角形三边长a，b，c 满足a²+c²=b²，那么以a，b，c 为三边的三角形是直角三角形，但是b为斜边。一定要记住，最长的边为斜边。

3、勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形。