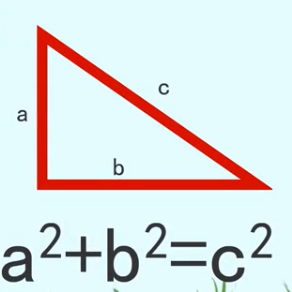
勾股定理推导方法-勾股定理相关题库与解答
勾股定理(英语:Pythagorean theorem),是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。最经典的勾股形就是两条直角边分别为3和4,斜边为5的直角三角形,有勾3股4弦5之称。
公式代表式:a²+b²=c²
更新时间:2024-04-24
勾股定理推导方法
勾股定理经典例题
-
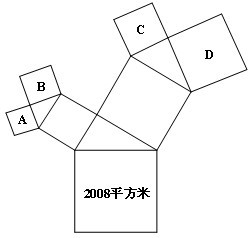
勾股定理练习题一
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,则正方形A,B,C,D的面积和为______。
-
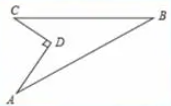
勾股定理练习题二
如图,在图形ABCD中,已知AD⊥CD,AD=4,CD=3,AB=13,BC=12,求图形ABCD的面积。
-
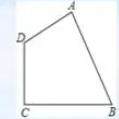
勾股定理练习题三
如图有四边形ABCD,已知AB=24,BC=15,CD=20,DA=7,BC⊥CD,求四边形ABCD的面积。
-
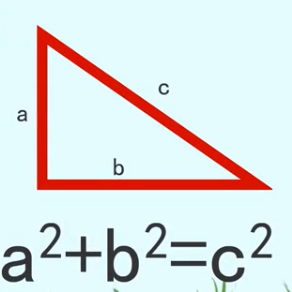
勾股定理练习题四
已知三角形ABC的三边分别为a、b、c,且满足a²+b²+c²+50=6a+8b+10c,求三角形ABC的面积。
-
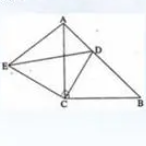
勾股定理练习题五
如图,三角形ACB和ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB上一点。
-

勾股定理与找规律综合练习题一
观察下列等式:3²+4²=5²,5²+12²=13²,7²+24²=25²,9²+40²=41²,按此规律,下一个等式是什么? 方法一 我们假设下一个等式为a²+b²=c²,通过观察我们发现: 1、等式的第一个数分别为3、5、7、9,是按顺序排列的奇数序列,因此判断下一个等式的第一个数为11,a=11。
-
勾股定理求最短距离之计算法
求平面中的最短距离有很多方法,本题为大家介绍最直接的一种方法,计算法。
-
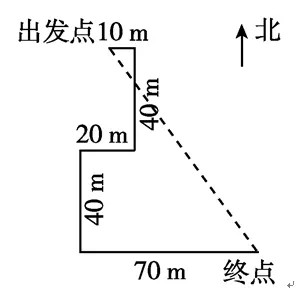
勾股定理求最短距离之平移法
如图,小明在广场上先向东走10 m,又向南走40 m,再向西走20 m,又向南走40 m,再向东走70 m.则小明到达的终点与原出发点的距离是________. 分析:连接出发点和终点,构造直角三角形,利用平移法及勾股定理求出出发点和终点两点之间的距离即可。
-

勾股定理求最短距离之对称法
如图,OA⊥OB,OA=45m,OB=15m,小明自A点出发沿着AO方向匀速驶向点O,小红同时从B处出发以相同的速度沿某直线去与小明在点C处相遇,(1)请用直尺和圆规作出C处的位置;(2)求BC的长度。
-
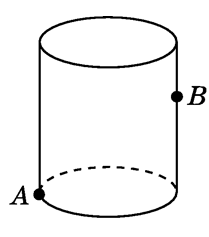
勾股定理求最短距离之展开法
有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图所示,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm。
-
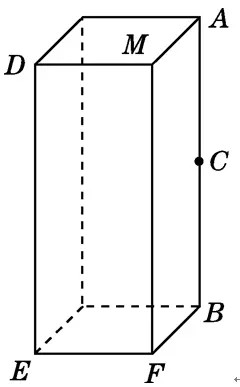
勾股定理求最短距离之展开法2
如图,桌子上放着一个长方体盒子,长、宽、高分别是12 cm,8 cm,30 cm,在AB的中点C处有一滴蜜糖,一只小虫从E处沿盒子表面爬到C处去吃.求小虫爬行的最短路程。
-
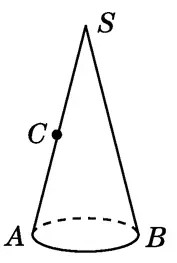
勾股定理求最短距离之展开法3
如图,观察图形解答下面的问题: (1)此图形的名称为________. (2)请你与同伴一起做一个这样的物体,并把它的侧面沿AS剪开,铺在桌面上,则它的侧面展开图是一个________. (3)如果点C是SA的中点,在A处有一只蜗牛,在C处恰好有蜗牛想吃的食物,但它又不能直接沿AC爬到C处,只能沿此立体图形的侧面爬行.你能在侧面展开图中画出蜗牛爬行的最短路线吗? (4)SA的长为10,侧面展开图的圆心角为90°,请你求出蜗牛爬行的最短路程. 解析 (1)此图形的名称为圆锥形。
勾股定理易错题
勾股定理题型解题技巧
- 05-10勾股定理的适用范围,只适用于直角三角形
- 05-10勾股定理的几个等式
- 05-11勾股定理的逆定理
- 05-10记住一些常用的勾股数有助于提高解题时的敏感度
- 05-11勾股定理在数学中可以用来解决哪些问题?
- 05-11勾股定理奇数组和偶数组口诀
- 05-12勾股定理的7个易错点
- 05-13奇数组勾股数和偶数组勾股数计算公式
勾股定理杂谈
- 05-06勾股定理的发展史及意义
- 05-08勾股定理的起源
- 05-08毕经与勾股定理
- 05-11勾股数顺口溜一
- 05-12勾股树,用勾股定理画出的毕达哥拉斯树
- 05-13勾股定理与数学海螺图



























